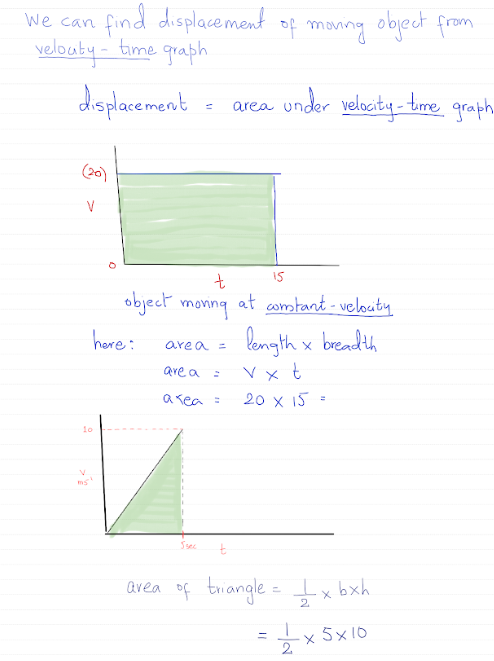
Average Speed
• Average speed tells how fast something moves during a time period.
– Average velocity is the overall velocity of a particle during a time interval. It tells how fast the position changed from the start to the end of that interval.
• It is found by dividing the total distance of an object divided by the total time taken to cover that displacement.
• The simple formula is:
\text{average speed} = \frac{\text{distance moved}}{\text{time taken}}
Unit of Speed
• The standard unit of speed is metre per second written as m.s-1.
Importance of Reference for Speed
• Speed has meaning only when compared to something fixed.
• Usually, speeds are taken relative to Earth’s surface.
• Even though Earth is moving in space, we often treat it as still for simple measurements.
• A person on a ferry may see a seagull flying beside the boat but appearing still.
• This means the seagull’s speed relative to the boat is zero.
• Even though the seagull is moving, it looks still to the passenger because it keeps pace with the boat.
Difference between speed and velocity
• In daily language, speed and velocity mean the same thing.
• In physics, they are different.
• Velocity tells how fast something moves and also the direction.
• Speed tells only how fast something moves.
• Speed is a scalar quantity, meaning it has no direction.
• Velocity is a vector quantity, meaning it includes direction.
Distance and displacement
• Distance is the total path covered by an object.
• Distance does not need direction.
• Displacement is the shortest distance between two points from a fixed frame of reference along linear direction.
• Displacement includes direction.
Average speed vs average velocity
• Average speed uses total distance.
• Average velocity uses displacement.
• They can be different because distance and displacement are different.
Definition of average velocity
• Average velocity is displacement divided by time taken.
• In math form:
\bar{v} = \frac{x_{2} - x_{1}}{t_{2} - t_{1}}
• The bar on top shows it is an average value.
• We can write displacement as Δx and time taken as Δt:
\bar{v} = \frac{\Delta x}{\Delta t}
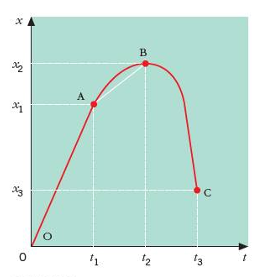
Understanding position–time graphs
• A position–time graph shows how the position of a particle changes with time.
• It gives a complete picture of the motion along a straight path.
• Example: From O to A, the particle moves with uniform velocity because the graph is a straight line
Interpreting parts of the graph
• O to A: Straight line means equal distances in equal times, so velocity is constant.
Average velocity in this part is
\frac{x_{1} - 0}{t_{1} - 0}
• A to B: The particle slows down because the slope of the graph decreases.
Average velocity here is
\frac{x_{2} - x_{1}}{t_{2} - t_{1}}
• B to C: The particle moves back toward the origin.
Since x₃ is less than x₂, the average velocity
\frac{x_{3} - x_{2}}{t_{3} - t_{2}}
is negative, showing reversed direction.
Limitations of average velocity
• Average velocity calculated over long intervals does not describe motion exactly.
• It only tells what happens overall, not at each instant.
• To understand the motion fully, we need velocity at every moment.
Instantaneous velocity
• Instantaneous velocity is the velocity at a specific moment.
• To find this, we take very small time intervals and calculate average velocity over those short intervals.
• As the time interval becomes extremely small, the short straight-line segment matches the slope of the curve at that point.
As the time interval becomes smaller and smaller, average velocity becomes closer to the velocity at that exact moment.
This leads to instantaneous velocity, which is the gradient of the tangent on a displacement–time graph.
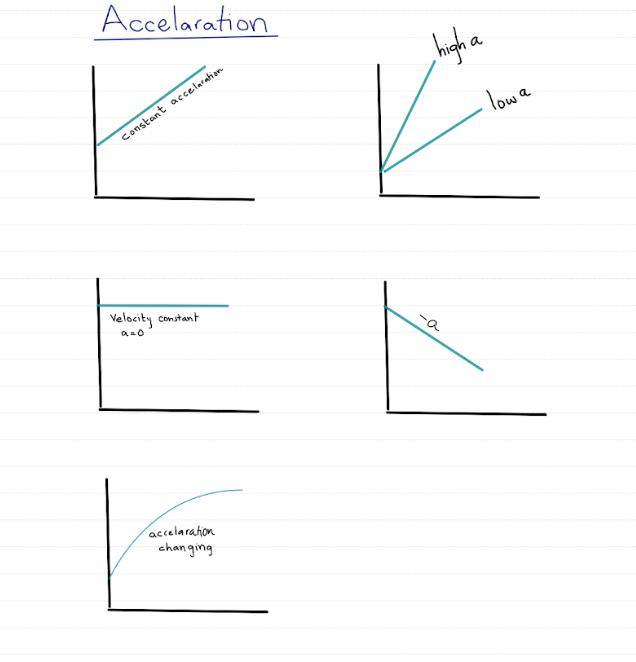
Instantaneous acceleration
• This is the acceleration at a single moment.
• Found by taking extremely small time intervals, similar to how instantaneous velocity is found.
• Since acceleration depends on change in velocity (a vector), acceleration is also a vector.
• That means it needs both magnitude and direction.
A familiar value of acceleration
• The acceleration due to gravity near Earth’s surface is 9.81 m s^(-2).
• In many cases it is taken as 10 m s^(-2) for simple calculations.
What uniformly accelerated motion means
• Uniform acceleration means acceleration stays constant with time.
• The kinematic equations describe motion when acceleration is constant.
• These equations apply to straight line motion.
• They do not apply to circular motion or simple harmonic motion.
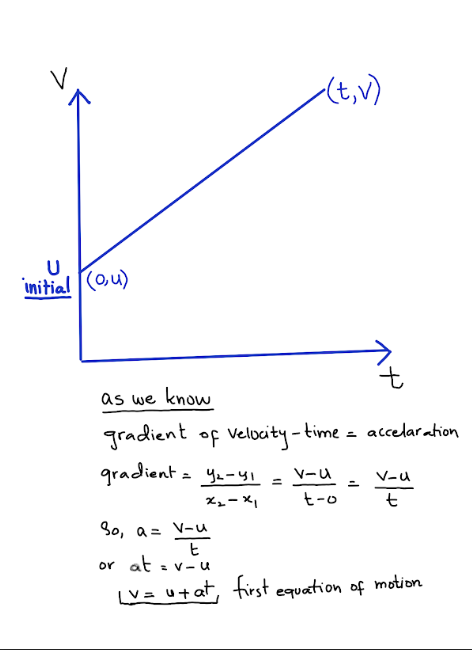
Basic relation between velocity and acceleration
• If the initial velocity at time t = 0 is u and after time t it becomes v,
then acceleration a is:
a = \frac{v - u}{t}
• Rearranging gives the basic velocity equation:
v = u + at
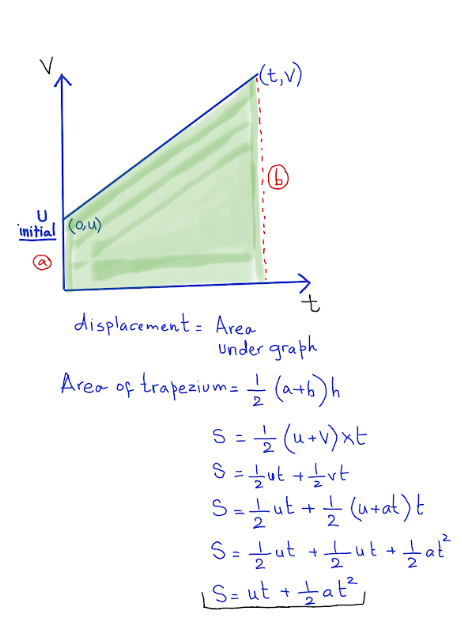
Distance travelled using average velocity
• Distance travelled s is average velocity multiplied by time.
• Average velocity is:
\bar{v} = \frac{u + v}{2}
• Using v = u + at, average velocity becomes:
\bar{v} = u + \frac{at}{2}
• So distance travelled becomes:
s = ut + \frac{1}{2} a t^{2}
Final velocity equation
• Another equation links final velocity v, initial velocity u, acceleration a and distance s:
v^{2} = u^{2} + 2as
• This equation is obtained by removing time from the earlier equations.
The five kinematic equations
These equations apply only when acceleration is constant.
- v = u + at
- s = ut + \frac{1}{2} a t^{2}
- s = vt - \frac{1}{2} a t^{2}
- v^{2} = u^{2} + 2as
- s = \bar{v} t = \frac{(u + v)t}{2}
EQUATIONS OF MOTION DERIVATION
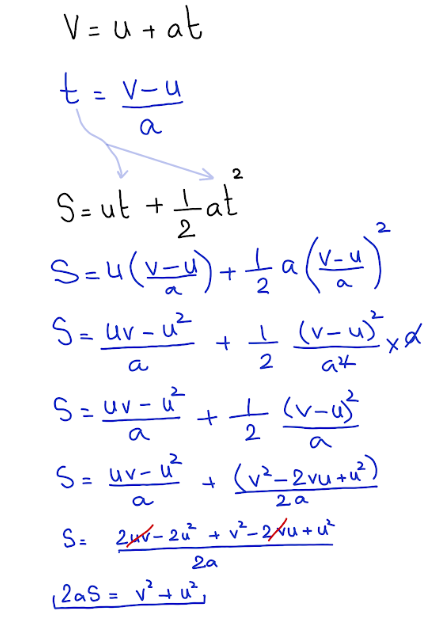
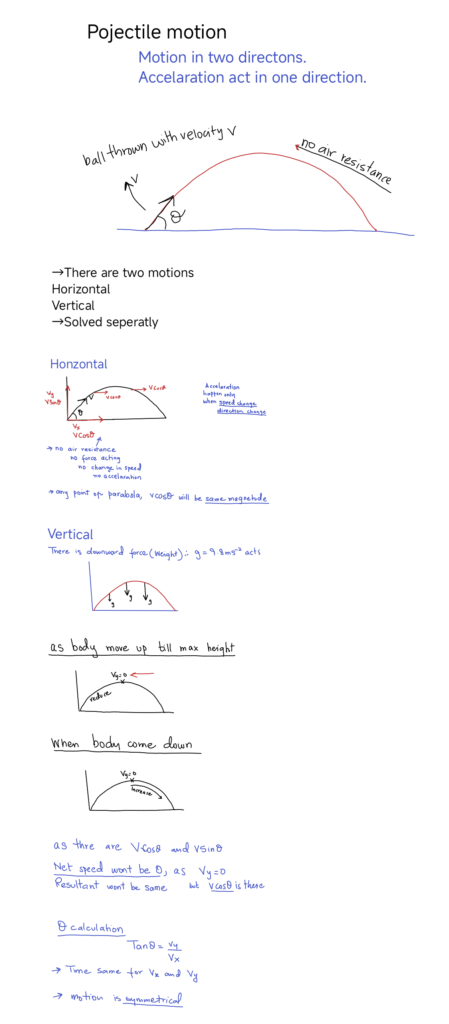
Motion with uniform velocity in one direction and uniform acceleration in a perpendicular direction
PROJECTILE