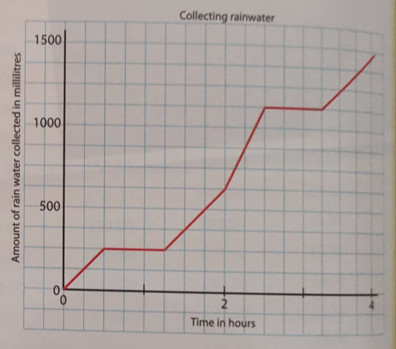
Question a: How much rainwater was collected between 2 hours and 2½ hours?
From the graph:
Each division is 125ml
- At 2 hours: 625ml collected
- At 2½ hours: 1125ml collected
- Answer: 1125 – 625 = 500ml
Question b: A further 562.5ml is collected between 4 hours and 5 hours. How much rainwater is there in the container now?
Steps:
- From graph at 4 hours: 1500ml
- Additional collected: 562.5ml
- Total = 1500 + 562.5 = 2062.5ml
Question c: 250ml of water was collected after 1 hour. How much more water was collected after 2 hours?
Steps:
- After 1 hour: 250ml
- After 2 hours (from graph): 500ml
- Additional water = 500 – 250 = 250ml more
Section 1: Solve (Mental Methods)
a) 4568 + 2980 Method: Add in parts
- 4568 + 3000 = 7568
- 7568 – 20 = 7548 Answer: 7548
b) 1608 – 528 Method: Subtract in parts
- 1608 – 500 = 1108
- 1108 – 28 = 1080 Answer: 1080
c) 4847 + 1253 Method: Add in parts
- 4847 + 1000 = 5847
- 5847 + 253 = 6100 Answer: 6100
d) 2003 – 1999 + 235 Method: Recognize patterns
- 2003 – 1999 = 4
- 4 + 235 = 239 Answer: 239
e) 8467 – 208 – 1467 Method: Rearrange and group
- 8467 – 1467 – 208
- 7000 – 208 = 6792 Answer: 6792
f) 753.6 – 248 + 46.4 Method: Look for pairs that make whole numbers
- 753.6 + 46.4 – 248
- 800 – 248 = 552 Answer: 552
Section 2: Create – Detailed Explanation
Looking at the grid of numbers provided: | 6974 | 2052 | | 9462 | 7462 | | 8476 | 725 | | 823 | 568 |
The task asks you to create addition and subtraction calculations using these numbers, then identify which mental method you used for each.
How to Approach This:
Step 1: Create Your Calculations
Pick any two numbers from the grid and create either an addition or subtraction problem.
Examples I’ll demonstrate:
Addition Problems:
- 823 + 725
- 2052 + 568
- 6974 + 2052
Subtraction Problems:
- 9462 – 7462
- 8476 – 6974
- 823 – 725 (this one is already shown in the table)
Step 2: Solve Using Mental Methods
Now I’ll show you how to solve each using the three mental methods mentioned:
Method 1: Rounding and Adjusting
Example: 823 + 725
- Round 823 to 800 (round down by 23)
- Round 725 to 700 (round down by 25)
- Add the rounded numbers: 800 + 700 = 1500
- Adjust: Add back what you took away: 1500 + 23 + 25 = 1548 Answer: 1548
Example: 8476 – 6974
- Round 8476 to 8500 (add 24)
- Round 6974 to 7000 (add 26)
- Subtract: 8500 – 7000 = 1500
- Adjust: 1500 + 24 – 26 = 1498 Answer: 1502 (Let me recalculate: 1500 – 2 = 1502)
Method 2: Partitioning and Sequencing
Example: 2052 + 568
- Break 568 into parts: 500 + 60 + 8
- Add in sequence:
- 2052 + 500 = 2552
- 2552 + 60 = 2612
- 2612 + 8 = 2620 Answer: 2620
Example: 9462 – 7462
- Notice the pattern: both numbers end in 462
- Subtract: 9000 – 7000 = 2000
- The 462s cancel out Answer: 2000
Method 3: Finding the Difference
Example: 823 – 725 (as shown in the table)
- Think: “How do I get from 725 to 823?”
- From 725 to 800 = 75
- From 800 to 823 = 23
- Total difference: 75 + 23 = 98 Answer: 98
Section 3: Measure
Measuring your table to nearest millimetre:
You need to physically measure your table, but here’s how to approach each part:
a) The difference between length and width:
- Measure length in mm
- Measure width in mm
- Subtract: length – width = difference
b) The perimeter of the table top:
- Perimeter = 2 × (length + width)
- Add all four sides together
c) Length of 5 same-sized tables placed end to end:
- Multiply table length × 5
Section 4: Investigate (Flight Tickets)
Problem: Flying with Fly Always costs £199 more than buying 2 tickets to the same destination with Star Choice Airline, where tickets cost less than £250.
To solve:
- Let Star Choice ticket cost = x (where x < £250)
- Cost of 2 Star Choice tickets = 2x
- Cost of 3 Fly Always tickets = 2x + £199
- Cost per Fly Always ticket = (2x + £199) ÷ 3
Find as many ways as possible:
- If Star Choice = £200, then 2 tickets = £400
- Fly Always total = £400 + £199 = £599
- Per Fly Always ticket = £599 ÷ 3 = £199.67
